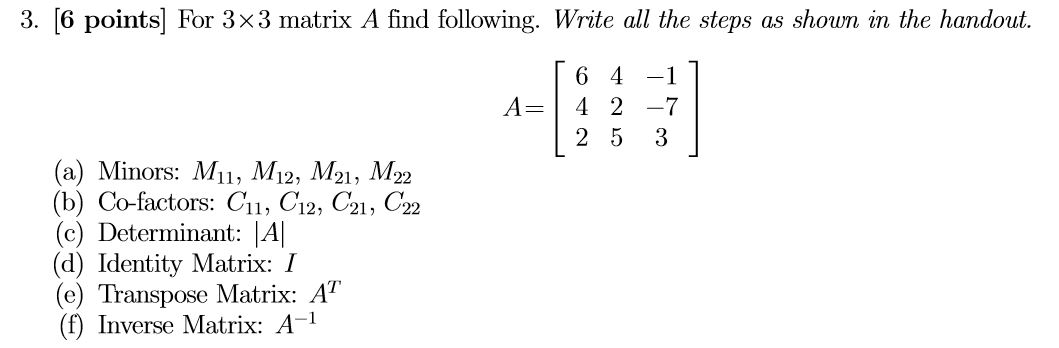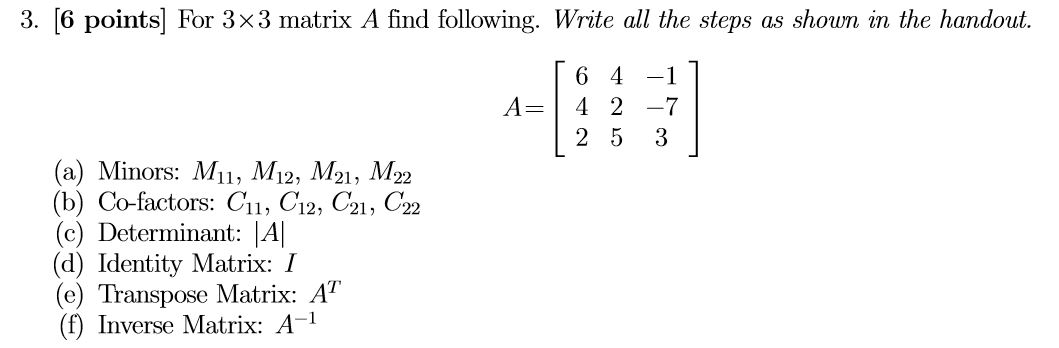Inverse Of Identity Matrix 3x3

Their product is the identity matrix which does nothing to a vector so a 1ax d x.

Inverse of identity matrix 3x3.

Any matrix that has a zero determinant is said to be singular meaning it is not invertible. A 3x3 identity matrix. When the identity matrix is the product of two square matrices the two matrices are said to be the inverse of each other. Ab ba i n then the matrix b is called an inverse of a.

Inverse of a matrix a is the reverse of it represented as a 1 matrices when multiplied by its inverse will give a resultant identity matrix. A 3x3 identity matrix. We look for an inverse matrix a 1 of the same size such that a 1 times a equals i. The identity matrix can also be written using the kronecker delta notation.

Here we are going to see some example problems of finding inverse of 3x3 matrix examples. It is square has same number of rows as columns. Whatever a does a 1 undoes. To compute the inverse of the matrix m we will write m and also write next to it the identity matrix an identity matrix is a square matrix with ones on the diagonal and zeros elsewhere.

A singular matrix is the one in which the determinant is not equal to zero. It s symbol is the capital letter i. We just mentioned the identity matrix. Finding inverse of 3x3 matrix examples.

What a matrix mostly does is to multiply. That is it is the only matrix such that. It is square has same number of rows as columns it has 1s on the diagonal and 0s everywhere else. It is the matrix equivalent of the number 1.

Elements of the matrix are the numbers which make up the matrix. The identity matrix is the matrix equivalent of the number 1. Matrices are array of numbers or values represented in rows and columns. If there exists a square matrix b of order n such that.

Next transpose the matrix by rewriting the first row as the first column the middle row as the middle column and the third row as the third column. To find the inverse of a 3 by 3 matrix is a little critical job but can be evaluated by following few steps. The identity matrix is the only idempotent matrix with non zero determinant. Finding inverse of 3x3 matrix examples.

A 3 x 3 matrix has 3 rows and 3 columns. But a 1 might not exist. If the determinant is 0 the matrix has no inverse. Let a be a square matrix of order n.

Inverse matrices 81 2 5 inverse matrices suppose a is a square matrix.